2024. 10. 3. 10:20ㆍSemiconductor setup/semiconductor theory


(3) 결정성 고체의 결정면과 결정 방향
결정성 고체는 원자들이 규칙적으로 배열되어 있어서 특정한 평면과 방향을 가집니다. 이때 **밀러 지수(Miller index)**라는 것을 사용하여 이러한 평면을 표시합니다. 밀러 지수는 다음과 같이 구합니다:
- 결정면이 x, y, z 축과 만나는 지점을 찾습니다. 만약 어떤 축과 만나지 않는다면, 그 지점은 '무한대(∞)'로 표시합니다.
- 각 만나는 지점의 역수를 취합니다. 즉, 1을 그 좌표 값으로 나눕니다.
- 그 결과를 소괄호로 묶어서 (hkl) 형태로 표시합니다.
예를 들어, 어떤 결정면이 x축과는 1에서 만나고, y축과 z축과는 만나지 않는다면, 그 만나는 지점은 (1, ∞, ∞)입니다. 각 좌표의 역수를 취하면 (1/1, 1/∞, 1/∞)이 되고, 이는 (1, 0, 0)이 됩니다. 따라서 이 결정면은 **(100)**으로 표시합니다.
또한, (010)과 (001) 같은 면들도 있는데, 이들은 각각 y축과 z축 방향에서 x축과 동일한 역할을 합니다. 이처럼 구조적으로 동일하지만 방향만 다른 면들을 **{100}**으로 묶어서 표시합니다.
결정 방향은 이러한 결정면에 수직인 방향을 나타내며, 대괄호로 묶어서 [hkl] 형태로 표시합니다. 예를 들어, (100) 면에 수직한 방향은 [100]입니다. 마찬가지로, [010], [001] 등의 방향도 있고, 이들을 모두 묶어서 **⟨100⟩**으로 표시합니다.
요약하자면:
- 밀러 지수(Miller index): 결정면을 나타내는 지표로, 각 축과의 교점을 역수로 취해 (hkl)로 표시합니다.
- {hkl} 표기법: 구조적으로 동일한 여러 면들을 묶어서 나타냅니다.
- [hkl] 표기법: 결정면에 수직한 방향을 나타냅니다.
- ⟨hkl⟩ 표기법: 구조적으로 동일한 여러 방향을 묶어서 나타냅니다.
이러한 표기법을 통해 결정 구조를 체계적으로 이해하고 표현할 수 있습니다.

'역수를 취한다'는 것은 어떤 수를 1로 나눈다는 뜻입니다.
밀러 지수를 구할 때 이 개념을 적용하는데, 단계별로 설명해드릴게요.
- 결정면이 x, y, z 축과 어디서 만나는지 찾습니다. 예를 들어, 결정면이 x축에서 2, y축에서 3, z축에서 무한대(축과 평행하다는 뜻입니다)에서 만난다고 해봅시다.
- 각 축과의 교점 값을 기록합니다.
- x축 교점: 2
- y축 교점: 3
- z축 교점: ∞ (무한대)
- 이 교점 값들의 역수를 구합니다.
- x축 역수: 1/2
- y축 역수: 1/3
- z축 역수: 1/∞ = 0 (무한대의 역수는 0입니다)
- 역수로 나온 값들을 최대한 간단한 정수로 변환합니다. 이를 위해 모든 역수 값을 공통된 수로 곱합니다. 이 예시에서는 6을 곱해볼게요.
- x축: (1/2) × 6 = 3
- y축: (1/3) × 6 = 2
- z축: 0 × 6 = 0
- 최종적으로 밀러 지수는 (3, 2, 0)이 됩니다.
요약하면, 역수를 취한다는 것은 각 축과의 교점 거리를 1로 나누어 그 값들을 이용해 밀러 지수를 구하는 과정입니다. 이 방법을 통해 결정면의 기하학적 특성을 간단한 숫자로 표현할 수 있습니다.
왜 역수를 취할까요?
- 결정면이 축과 가까이 만날수록 역수를 취한 값은 커집니다.
- 결정면이 축과 멀리 만날수록(또는 평행할수록) 역수를 취한 값은 작아집니다(또는 0이 됩니다).
- 이렇게 하면 결정면의 기울기나 방향을 단순한 정수 비율로 나타낼 수 있어 분석과 표현이 쉬워집니다.
추가 예시:
- 만약 결정면이 x축에서 1, y축에서 ∞, z축에서 ∞에서 만난다면:
- 교점: (1, ∞, ∞)
- 역수: (1/1, 1/∞, 1/∞) = (1, 0, 0)
- 밀러 지수: (100)
즉, '역수를 취한다'는 것은 결정면과 각 축의 관계를 간단한 수로 표현하기 위한 수학적 방법입니다.
반도체로 사용되는 실리콘은 전자의 흐름을 제어하는 중요한 소재입니다. 이 실리콘을 만들 때는 **특정한 결정면(평면)**과 결정 방향을 선택합니다. 왜 그럴까요? 그 이유는 결정 방향에 따라 전자 소자의 성능이 달라지기 때문입니다.
대량 생산되는 실리콘 웨이퍼는 일반적으로 (100) 면을 사용합니다. 이 면을 사용하면 소자의 특성이 균일하고 안정적이어서 좋은 품질의 제품을 만들 수 있습니다.
또한, 실리콘 소자의 핵심인 MOSFET이라는 소자가 있습니다. 이 소자의 성능을 최적화하기 위해 [100] 방향이나 [110] 방향이 MOSFET 소자를 가로지르도록 방향을 맞춥니다. 이렇게 하면 소자가 더 효율적으로 작동합니다.
웨이퍼에서 이러한 방향을 정확히 맞추기 위해 표시를 해두는데, 이것을 **'평탄면(Flat zone)'**이나 **'새김눈(Notch)'**이라고 부릅니다. 이는 웨이퍼의 가장자리에 있는 작은 표시나 홈입니다.
특히 대량 생산에서는 웨이퍼의 사용 가능한 면적을 최대한 활용하기 위해 **'새김눈(Notch)'**을 많이 사용합니다. 이는 웨이퍼의 낭비를 줄여 생산 효율을 높여줍니다.
정리하면:
- 실리콘 웨이퍼는 특정한 평면과 방향을 선택하여 제작됩니다.
- 이는 소자의 성능을 향상시키기 위한 것입니다.
- 방향을 맞추기 위해 **표시(평탄면 또는 새김눈)**를 합니다.
- 새김눈은 웨이퍼의 면적 낭비를 줄여주어 생산성을 높입니다.
이렇게 함으로써 반도체 소자의 품질과 효율을 높일 수 있습니다.

2. 에너지 밴드 이론
1. 에너지 밴드
(1) 에너지 밴드와 원자 간 거리
쉽게 설명해 드릴게요:
- *실리콘(Si)**은 원자 번호 14번인 원소로, 주기율표에서 4족 원소에 속합니다. 이는 실리콘이 최외각 껍질에 4개의 전자를 가지고 있다는 뜻입니다. 이 전자들은 원자 간 결합과 전기적 성질에 중요한 역할을 합니다.
전자 배치를 보면, 실리콘 원자는 다음과 같이 전자들이 배치되어 있습니다:
- 1s² 2s² 2p⁶ 3s² 3p²
이것은 각 에너지 준위(껍질)에 전자들이 어떻게 채워져 있는지를 보여줍니다:
- 1s²: 가장 낮은 에너지 껍질에 전자 2개
- 2s² 2p⁶: 그 다음 에너지 껍질에 전자 8개
- 3s² 3p²: 가장 바깥쪽 에너지 껍질(최외각)에 전자 4개
훈트의 법칙에 따르면, 같은 에너지 준위 내의 오비탈은 먼저 각 오비탈에 한 개의 전자를 채우고, 그 다음에 짝을 이루게 됩니다. 하지만 실리콘의 경우 3s 오비탈은 에너지가 낮아 전자 2개가 모두 채워지고, 3p 오비탈에는 전자 2개가 각각 다른 오비탈에 하나씩 채워집니다.
그림 2-20에서는 이러한 전자 배치를 시각적으로 보여주는데요:
- 3s 오비탈: 전자 2개로 꽉 차 있음
- 3p 오비탈: 3개의 p 오비탈 중 2개에 전자 1개씩 존재
여기서 중요한 점은 3p 오비탈이 3s 오비탈보다 에너지가 높다는 것입니다. 즉, 3p 오비탈의 전자들은 3s 오비탈의 전자들보다 더 높은 에너지 상태에 있습니다.
핵심 정리:
- 실리콘 원자는 최외각에 4개의 전자를 가지고 있으며, 이는 다른 원자들과 결합할 때 사용됩니다.
- 전자들의 에너지 수준은 원자의 고유한 성질을 결정하며, 원자들이 모여서 고체를 이루면 이 에너지 수준들이 서로 겹치면서 에너지 밴드를 형성합니다.
- 에너지 밴드는 고체에서 전자들이 가질 수 있는 에너지의 범위를 나타내며, 이는 전기 전도성과 같은 물질의 성질에 큰 영향을 줍니다.
쉽게 말해, 실리콘 원자 하나에서는 전자들이 특정한 에너지 수준에 위치하지만, 여러 개의 실리콘 원자들이 가까워져서 고체를 이루면 이 전자 에너지 수준들이 서로 겹치게 됩니다. 그 결과로 에너지 밴드라는 연속적인 에너지 영역이 형성됩니다. 이 에너지 밴드는 전자들이 어떻게 움직일 수 있는지를 결정하며, 이는 반도체의 중요한 특성 중 하나입니다.
비전공자도 이해할 수 있게 요약하면:
- 실리콘은 4개의 바깥쪽 전자를 가지고 있는 원자입니다.
- 이 전자들은 에너지 수준에 따라 자리를 잡고 있습니다.
- 여러 실리콘 원자가 모이면 이 전자들의 에너지 수준이 겹쳐서 에너지 밴드가 됩니다.
- 이 에너지 밴드는 전자의 이동과 전기적 성질에 큰 영향을 미칩니다.
이렇게 해서 실리콘의 전자 배치와 에너지 밴드에 대해 간단히 설명해 드렸습니다.
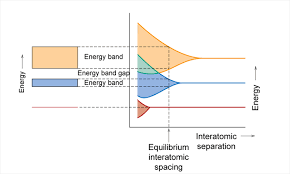
에너지 밴드와 실리콘 원자 간 거리
쉽게 설명해 드릴게요:
1. 실리콘 원자의 격자 구조와 상호작용
- 실리콘(Si) 원자들이 모여 격자 구조를 형성하면, 각 원자들이 서로 상호작용을 하게 됩니다.
- 이때, 원자들 사이의 거리가 가까워지면서 전자들의 위치가 겹치기 시작합니다.
2. 전자들의 에너지 준위 변화와 에너지 밴드의 형성
- 파울리의 배타 원리에 따르면, 하나의 에너지 준위에는 하나의 전자만 존재할 수 있습니다.
- 그래서 전자들이 겹치지 않기 위해, 각 전자의 에너지 준위가 조금씩 달라지면서 배치됩니다.
- 이렇게 수많은 에너지 준위들이 아주 가까운 에너지 값으로 촘촘히 배열되면, 이것이 마치 **띠(band)**처럼 보입니다.
- 이러한 띠를 **에너지 밴드(Energy Band)**라고 합니다.
3. 에너지 밴드와 원자 간 거리의 관계
- 에너지 밴드는 원자 간 거리에 따라 형성되는 방식이 달라집니다.
- 원자들이 무한히 멀리 떨어져 있을 때는 서로 영향을 주지 않으므로, 전자들은 고유한 에너지 준위를 가집니다.
- 원자들이 점점 가까워지면:
- 상호 인력(원자핵과 전자 사이의 인력)에 의해 위치 에너지가 감소합니다.
- 시스템이 더 안정한 상태로 바뀝니다.
4. 최적의 원자 간 거리와 결합 길이
- 그러나 원자들이 너무 가까워지면:
- 원자핵 사이의 반발력이 급격히 증가합니다.
- 이로 인해 위치 에너지가 다시 증가하고, 시스템이 불안정해집니다.
- 따라서 가장 안정한 상태를 이루는 특정한 원자 간 거리가 존재합니다.
- 이 거리를 **결합 길이(Bond Length)**라고 부릅니다.
- 실리콘의 결합 길이는 약 **2.35Å(옹스트롬)**입니다.
- *1Å(옹스트롬) = 0.1 나노미터(nm)**로 아주 작은 길이의 단위입니다.
5. 왜 이것이 중요한가요?
- 에너지 밴드의 형성은 물질의 전기적 성질을 결정합니다.
- 반도체인 실리콘에서 에너지 밴드는 전자가 어떻게 이동할 수 있는지를 나타내며, 이는 전기 전도도와 밀접한 관련이 있습니다.
- 에너지 밴드 구조를 이해하면, 왜 어떤 물질은 전기가 통하고(도체), 어떤 물질은 전기가 통하지 않으며(절연체), 또 어떤 물질은 **그 중간 성질(반도체)**을 가지는지 알 수 있습니다.
정리하면:
- 실리콘 원자들이 가까워지면서 전자들의 에너지 준위가 겹치지 않도록 조금씩 변형되어 에너지 밴드를 형성합니다.
- 원자 간 거리는 이 에너지 밴드의 형성에 큰 영향을 미치며, 가장 안정한 거리를 결합 길이라고 합니다.
- 실리콘의 결합 길이는 2.35Å로, 이 거리에서 실리콘 원자들은 가장 안정적으로 존재합니다.
- 이러한 개념은 반도체 기술의 기반이 되며, 전자의 이동과 물질의 전기적 특성을 이해하는 데 필수적입니다.
추가로 알아두면 좋은 점:
- 에너지 밴드 구조는 전자공학과 재료공학에서 매우 중요한 개념입니다.
- 반도체 소자(예: 트랜지스터, 다이오드)는 에너지 밴드의 특성을 활용하여 전류를 제어합니다.
- 에너지 갭(Energy Gap): 에너지 밴드 사이의 간격으로, 전자의 이동 여부를 결정합니다.
한마디로 말해서:
- 실리콘 원자들이 모여서 격자 구조를 이루면, 전자들이 서로 겹치지 않기 위해 에너지 준위를 조금씩 바꾸어 에너지 밴드를 형성합니다.
- 원자 간의 거리가 적절해야 시스템이 안정하며, 이때의 거리를 결합 길이라고 합니다.
- 이러한 원리로 인해 실리콘은 반도체로서의 성질을 가지게 되며, 이는 현대 전자기기의 핵심이 됩니다.
(2) 실리콘 격자에서의 에너지 밴드
쉽게 설명해 드릴게요:
1. 실리콘 원자의 격자 구조
- N개의 실리콘 원자가 모여 **격자(lattice)**를 이룹니다.
- 이 격자 안에서 전자들의 에너지 수준을 살펴보겠습니다.
2. 에너지 레벨과 밴드 형성
- 1s, 2s, 2p 에너지 레벨은 **전자가 가득 찬 상태(Filled state)**입니다.
- 이 레벨들은 이미 전자들로 꽉 차 있어서 에너지 밴드를 형성하지 않습니다.
- 최외각 전자 바깥쪽의 에너지 레벨(예: 3d, 4s 등)은 **전자가 없는 상태(Empty state)**입니다.
- 이 레벨들은 전자가 없기 때문에 격자의 전자 구조에 큰 영향을 주지 않습니다.
3. 중요한 에너지 레벨: 3s와 3p
- 최외각 에너지 레벨인 3s와 3p는 특별한 역할을 합니다.
- 이 레벨들은 상위 4N개와 하위 4N개의 에너지 레벨로 나뉩니다.
- 여기서 N은 실리콘 원자의 개수를 의미합니다.
- 실리콘은 총 4N개의 최외각 전자를 가지고 있습니다.
- 이 전자들은 하위 4N개의 에너지 레벨에 모두 채워집니다.
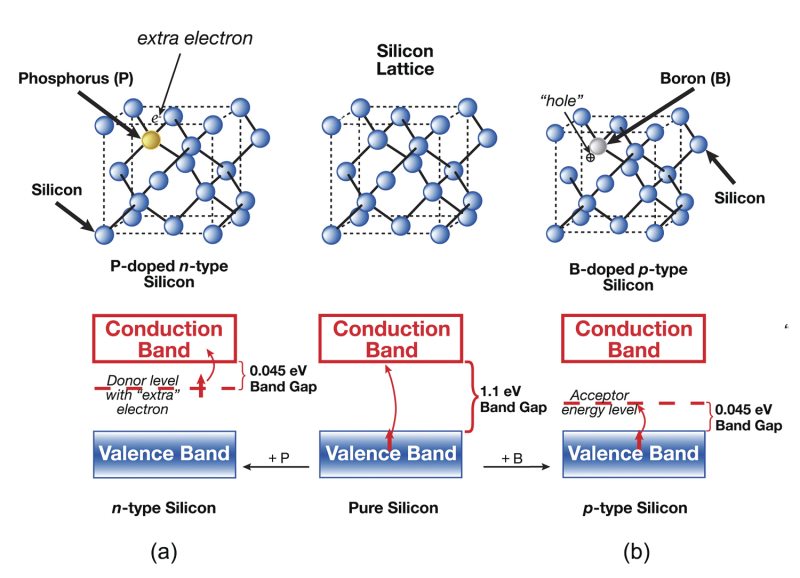
- 이 하위 에너지 레벨을 **가전자대(Valence Band)**라고 부릅니다.
- 반대로, 상위 4N개의 에너지 레벨은 전자가 없는 빈 상태입니다.
- 이 상위 레벨을 **전도대(Conduction Band)**라고 합니다.
4. 금지대와 밴드갭
- 가전자대와 전도대 사이에는 전자가 존재할 수 없는 영역이 있습니다.
- 이 영역을 **금지대(Forbidden Band)**라고 합니다.
- 금지대의 폭은 **전도대의 하단 에너지(E<sub>c</sub>)**와 **가전자대의 상단 에너지(E<sub>v</sub>)**의 차이로 결정됩니다.
- 이 에너지 차이를 **밴드갭 에너지(Bandgap Energy)**라고 부릅니다.
- 실리콘의 밴드갭 에너지는 약 **1.12eV(전자볼트)**입니다.
- 이 값은 전자가 가전자대에서 전도대로 넘어가기 위해 필요한 에너지입니다.
5. 왜 이것이 중요한가요?
- 에너지 밴드 구조는 물질의 전기적 성질을 결정합니다.
- 가전자대(Valence Band):
- 전자들로 가득 차 있어 전류를 잘 흐르게 하지 않습니다.
- 전도대(Conduction Band):
- 전자가 없지만, 전자가 들어오면 전류를 흐르게 할 수 있습니다.
- 금지대(Forbidden Band):
- 전자가 존재할 수 없는 영역으로, 전자의 이동을 제어합니다.
- 밴드갭 에너지가 작으면:
- 전자가 적은 에너지로도 전도대에 올라갈 수 있어 전기 전도성이 높아집니다.
- 밴드갭 에너지가 크면:
- 전자가 전도대로 넘어가기 어려워 절연체가 됩니다.
- 실리콘의 경우:
- *밴드갭 에너지(1.12eV)**가 중간 정도여서, 반도체로 작동합니다.
- 외부 에너지(열, 빛 등)를 받으면 전자가 전도대로 이동하여 전류가 흐를 수 있습니다.
요약하면:
- 실리콘 격자에서는 최외각 전자들이 가전자대를 형성하고, 그 위에는 전자가 없는 전도대가 있습니다.
- *가전자대와 전도대 사이의 금지대(밴드갭)**는 전자의 이동을 막거나 허용하는 역할을 합니다.
- *실리콘의 밴드갭 에너지(1.12eV)**는 반도체로서의 성질을 가능하게 하여, 전자 소자로 활용됩니다.
쉽게 말해,
- 에너지 밴드 구조는 전자가 물질 내에서 어떻게 움직일 수 있는지를 결정합니다.
- 실리콘은 이러한 구조 덕분에 전기 전도성을 조절할 수 있어, 컴퓨터 칩이나 트랜지스터 같은 전자 기기에 널리 사용됩니다.
추가로 알아두면 좋은 점:
- 전자가 가전자대에서 전도대로 이동하면, 물질은 전류를 흐르게 됩니다.
- 외부 에너지(예: 열, 빛)를 가하면 이 이동이 촉진됩니다.
- 반도체의 특성을 이해하면 전자 공학의 기본 원리를 알 수 있습니다.
그래서 결론적으로,
- 실리콘의 에너지 밴드 구조는 반도체 기술의 핵심이며, 이를 통해 현대의 다양한 전자 기기가 작동할 수 있습니다.
2. 에너지 밴드에서의 전기 전도
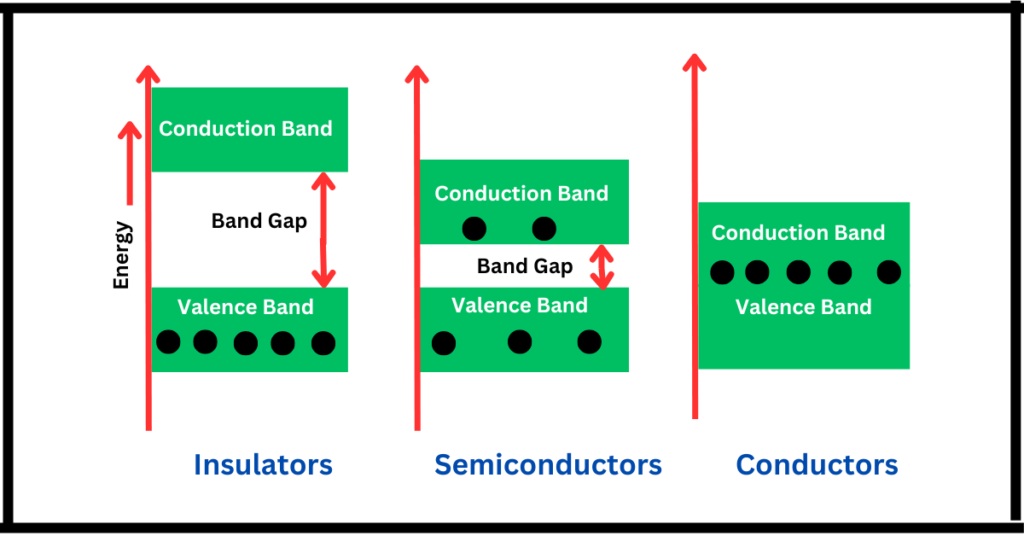
전류가 흐르려면 어떻게 해야 할까요?
- 전류는 전자의 움직임으로 발생합니다.
- 전기장이 외부에서 가해졌을 때, 전자들이 **'의미 있는 이동'**을 해야 전류가 흐릅니다.
가전자대(Valence Band)란?
- 가전자대는 전자가 가득 차 있는 에너지 영역입니다.
- 여기의 전자들은 원자핵에 단단히 묶여 있어서 자유롭게 움직일 수 없습니다.
- 또한, 가전자대는 전자가 이미 꽉 차 있어서, 어떤 전자가 한 방향으로 움직여도 반대 방향으로 움직이는 전자가 있어서 전체적인 전류는 0이 됩니다.
- 결론적으로, 가전자대의 전자들은 전류에 기여하지 않습니다.
전도대(Conduction Band)란?
- 전도대는 전자가 거의 없거나 완전히 비어 있는 에너지 영역입니다.
- 전자가 전혀 없다면 당연히 전류가 흐르지 않습니다.
- 그러나 전도대에 전자가 존재하면, 이 전자들은 원자핵에 묶여 있지 않아서 자유롭게 이동할 수 있습니다.
- 이러한 전자를 자유전자라고 부릅니다.
- 자유전자는 외부 전기장에 반응하여 이동하므로, 전류를 흐르게 합니다.
정공(Hole)이란?
- 가전자대에서 어떤 이유로 전자 하나가 전도대로 이동하면, 가전자대에는 전자 하나의 빈자리가 생깁니다.
- 이 빈자리를 **정공(hole)**이라고 합니다.
- 정공은 양전하를 가진 입자처럼 행동하며, 주변 전자들이 이 빈자리를 채우기 위해 이동하게 됩니다.
- 정공의 이동도 전류를 흐르게 하는 데 기여합니다.
왜 이것이 중요한가요?
- 전기 전도성은 자유롭게 움직일 수 있는 전하 운반자(자유전자와 정공)가 있을 때 가능합니다.
- 금속에서는 전도대에 전자가 많이 있어서 전류가 잘 흐릅니다.
- 반도체에서는 온도나 빛 등의 외부 에너지로 인해 전자들이 전도대로 올라가서 전류를 흐르게 할 수 있습니다.
- 절연체는 전도대에 전자가 거의 없고, 전도대와 가전자대 사이의 에너지 차이가 커서 전류가 거의 흐르지 않습니다.
한마디로 정리하면:
- 전류가 흐르기 위해서는 전도대에 있는 자유전자가 필요합니다.
- 가전자대의 전자들은 움직일 수 없지만, 전도대로 올라간 전자들은 자유롭게 움직일 수 있습니다.
- 자유전자의 움직임과 정공의 이동이 전류의 흐름을 만들어냅니다.
이해를 돕기 위한 비유:
- 가전자대의 전자들은 좌석이 꽉 찬 극장의 관객과 같습니다. 아무도 움직일 수 없고, 움직여도 옆 사람과 부딪혀서 전체적인 이동이 없습니다.
- 전도대의 자유전자는 빈 운동장에서 뛰어노는 아이들과 같습니다. 자유롭게 이곳저곳으로 이동할 수 있습니다.
- 정공은 열쇠를 잃어버린 사람처럼, 주변 사람들이 그 열쇠를 찾기 위해 여기저기 움직이는 상황과 비슷합니다.
결론적으로:
- 전류는 자유롭게 움직일 수 있는 전하(전자나 정공)가 있을 때 흐릅니다.
- 반도체 기술은 이러한 원리를 이용하여 전자 기기를 만들고 작동시킵니다.
3. 에너지 밴드에 따른 물질 분류
에너지 밴드를 통한 물질의 분류
물질은 **에너지 밴드갭(Bandgap)**의 크기에 따라 세 가지로 분류할 수 있습니다:
- 밴드갭이 작거나 겹치는 물질
- *가전자대(Valence Band)**와 전도대(Conduction Band) 사이의 에너지 차이가 매우 작거나 아예 겹쳐 있습니다.
- 전자들이 쉽게 이동할 수 있어 전류가 잘 흐릅니다.
- 이러한 물질을 **도체(Conductor)**라고 합니다.
- 예시: 구리, 은, 금과 같은 금속들.
- 적당한 밴드갭을 가진 물질
- 가전자대와 전도대 사이에 중간 정도의 에너지 차이가 있습니다.
- 외부 에너지(열, 빛 등)를 받으면 전자들이 전도대로 이동할 수 있습니다.
- 이러한 물질을 **반도체(Semiconductor)**라고 합니다.
- 예시: 실리콘(Si), 갈륨 비소(GaAs).
- 큰 밴드갭을 가진 물질
- 가전자대와 전도대 사이의 에너지 차이가 매우 큽니다.
- 전자들이 전도대로 이동하기 어렵기 때문에 전류가 거의 흐르지 않습니다.
- 이러한 물질을 **부도체(Insulator)**라고 합니다.
- 예시: 유리, 고무, 다이아몬드.
밴드갭이 전기 전도성에 미치는 영향
- 밴드갭이 작거나 없는 경우:
- 전자들이 자유롭게 이동하여 전류가 잘 흐릅니다.
- 도체의 특징입니다.
- 밴드갭이 큰 경우:
- 전자들이 전도대로 이동하기 어려워 전류가 잘 흐르지 않습니다.
- 부도체의 특징입니다.
- 밴드갭이 중간인 경우:
- 외부 에너지를 가하면 전자들이 전도대로 이동할 수 있어 전기적 성질을 조절할 수 있습니다.
- 반도체의 특징입니다.
반도체와 부도체의 구분 기준
- 명확한 경계는 없지만, 일반적으로 밴드갭 에너지로 구분합니다.
- 반도체의 상위 한계는 **밴드갭이 약 3.4eV인 갈륨 나이트라이드(GaN)**로 봅니다.
- 밴드갭이 3.4eV 이상이면 부도체로 분류합니다.
왜 이것이 중요한가요?
- 반도체는 전자 기기의 핵심 재료로 사용됩니다.
- 에너지 밴드 구조를 이해하면 물질의 전기적 특성을 예측하고 조절할 수 있습니다.
- 이는 트랜지스터, 다이오드 등 전자 소자의 동작 원리를 이해하는 데 필수적입니다.
정리하면:
- 물질은 에너지 밴드갭의 크기에 따라 도체, 반도체, 부도체로 분류됩니다.
- 도체: 밴드갭이 작거나 없어 전류가 잘 흐름.
- 반도체: 밴드갭이 중간으로, 외부 에너지로 전기적 성질을 조절 가능.
- 부도체: 밴드갭이 커서 전류가 거의 흐르지 않음.
이해를 돕기 위한 비유
- 도체는 넓은 길과 같아서 자동차(전자)가 자유롭게 달릴 수 있습니다.
- 부도체는 벽으로 막힌 길과 같아서 자동차가 갈 수 없습니다.
- 반도체는 차단기가 있는 길과 같아서, 차단기를 열어주면 자동차가 지나갈 수 있습니다.
이렇게 해서 에너지 밴드에 따른 물질의 분류를 쉽게 이해할 수 있습니다.
4. 비평형 상태에서의 에너지 밴드
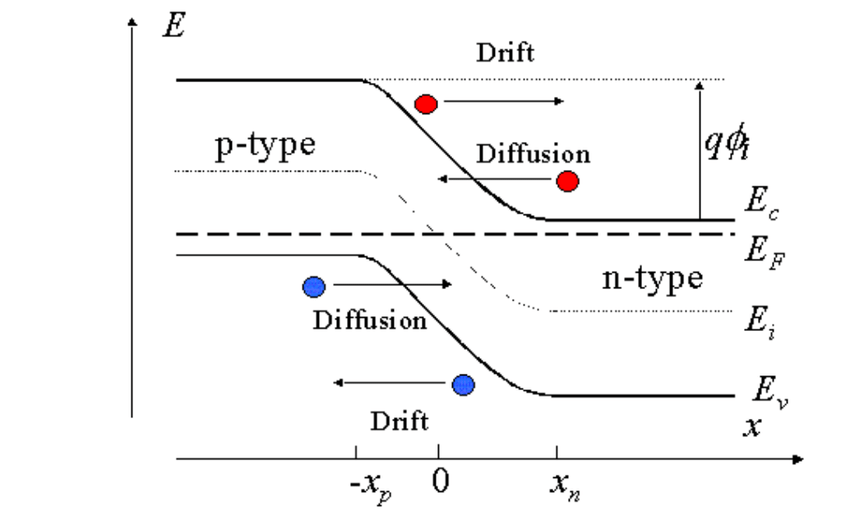
1. 에너지 레벨과 위치 에너지
- 에너지 레벨은 전자들이 가질 수 있는 에너지 상태를 말합니다.
- 낮은 에너지 레벨에 있는 전자는 원자핵에 더 가까이 있습니다.
- 이는 전자가 낮은 위치 에너지를 가지고 있다는 뜻입니다.
- 쉽게 말해, 전자가 에너지적으로 안정된 상태에 있다는 것입니다.
2. 외부에서 전압을 가하면 무슨 일이 일어날까요?
- 이제 **외부에서 전압(전기장)**을 걸어줍니다.
- 양전압(플러스 전압)을 한쪽에 가하면, 전자는 음전하를 띠기 때문에 양전압이 가해진 쪽으로 끌려갑니다.
- 즉, 전자는 전압이 인가된 방향으로 이동합니다.
- 전자가 이동하면서 위치 에너지가 어떻게 변할까요?
- 전자는 양전압 쪽으로 이동하면서 위치 에너지가 감소합니다.
- 이는 전자가 에너지적으로 더 안정된 상태로 가는 것을 의미합니다.
3. 에너지 밴드로 표현하면 어떻게 될까요?
- 에너지 밴드 그림은 전자들의 에너지 상태를 보여주는 도구입니다.
- 세로 축은 에너지를 나타냅니다.
- 가로 축은 공간적 위치나 원자 구조를 나타냅니다.
- 전압을 가하지 않은 상태에서는 에너지 밴드가 일정한 높이로 평평하게 그려집니다.
- 전압을 가하면:
- 전자의 위치 에너지가 감소하므로, 에너지 밴드 전체가 아래로 내려갑니다.
- 이는 전자가 더 낮은 에너지 상태로 이동했다는 것을 시각적으로 보여줍니다.
4. 왜 에너지 밴드가 전체적으로 하강할까요?
- 전압을 가하면 전기장이 형성되고, 이는 물질 내에서 전자의 에너지 상태를 변화시킵니다.
- 에너지 밴드의 하강은 전자가 에너지적으로 더 낮은 상태로 이동했음을 나타냅니다.
- 즉, 전자가 양전압 방향으로 이동하면서 에너지를 잃었다는 뜻입니다.
5. 이해를 돕기 위한 비유
- 전자를 공 위에 있는 공으로 생각해 봅시다.
- 전압을 가하지 않은 상태에서는 공이 평평한 테이블 위에 있습니다.
- 전압을 가하면 테이블이 한쪽으로 기울어집니다.
- 공은 **낮은 쪽(양전압 쪽)**으로 굴러가게 되며, 이는 위치 에너지의 감소를 의미합니다.
- 에너지 밴드가 기울어지는 것은 테이블이 기울어진 것과 같은 이치입니다.
6. 핵심 요약
- 전압을 가하면 전기장이 형성되고, 전자는 양전압 방향으로 이동합니다.
- 전자의 위치 에너지는 감소하며, 이는 에너지 밴드 다이어그램에서 밴드가 내려가는 것으로 표현됩니다.
- 에너지 밴드의 하강은 물질 내에서 전자들의 에너지 상태 변화를 시각적으로 보여줍니다.
7. 왜 이것이 중요한가요?
- 전자 소자(예: 다이오드, 트랜지스터)에서 전압을 가하는 것은 기본적인 동작 원리입니다.
- 에너지 밴드 다이어그램을 통해 전자들의 에너지 변화와 이동 방향을 쉽게 이해할 수 있습니다.
- 이는 전류의 흐름과 전자 소자의 작동 방식을 이해하는 데 필수적입니다.
결론적으로:
- 외부 전압을 가하면, 전자의 위치 에너지가 감소하고, 이는 에너지 밴드의 전체적인 하강으로 나타납니다.
- 이러한 변화는 전자들의 이동과 전류의 흐름을 설명하는 데 중요한 역할을 합니다.
(실리콘) 반도체의 에너지 밴드 다이어그램을 설명하세요.
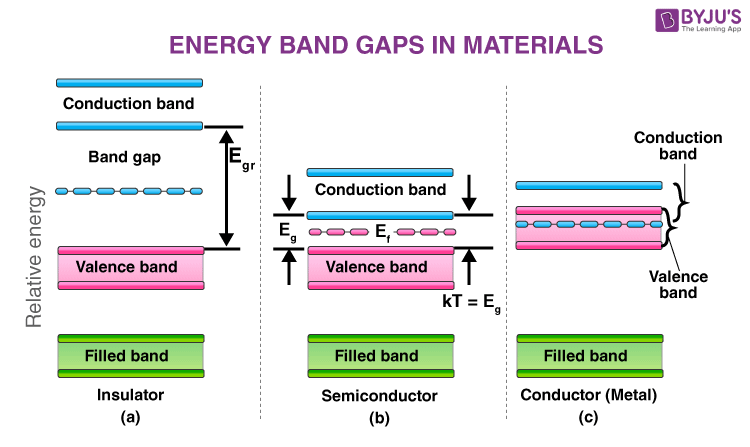
실리콘 반도체의 에너지 밴드 다이어그램은 반도체의 전기적 특성과 동작 원리를 이해하는 데 핵심적인 역할을 합니다.
1. 에너지 밴드 구조:
- 가전자대 (Valence Band): 실리콘 원자의 최외각 전자들이 차지하는 에너지 영역입니다. 이 전자들은 원자와 강하게 결합되어 있어 이동이 제한적이며, 일반적으로 전류에 기여하지 않습니다.
- 전도대 (Conduction Band): 가전자대보다 높은 에너지 영역으로, 여기의 전자들은 원자 결합에서 벗어나 자유롭게 이동할 수 있습니다. 이러한 전자들은 전기 전도에 직접적으로 기여합니다.
- 밴드갭 (Band Gap): 가전자대와 전도대 사이의 에너지 차이로, 전자가 가전자대에서 전도대로 이동하기 위해 극복해야 하는 최소 에너지입니다. 실리콘의 밴드갭은 약 1.12 eV입니다.
2. 에너지 밴드 다이어그램의 해석:
- 순수한 실리콘 (Intrinsic Semiconductor): 절대 영도에서는 가전자대가 전자로 완전히 채워져 있고, 전도대는 비어 있습니다. 이 상태에서는 전기 전도가 거의 일어나지 않습니다.
- 열적 여기: 온도가 상승하면 열 에너지로 인해 일부 전자들이 밴드갭을 넘어 전도대로 이동합니다. 이로써 전도대에는 자유전자가, 가전자대에는 **정공(hole)**이 생성되어 전류가 흐를 수 있게 됩니다.
- 도핑 (Doping): 실리콘에 불순물을 첨가하여 전기적 특성을 조절할 수 있습니다.
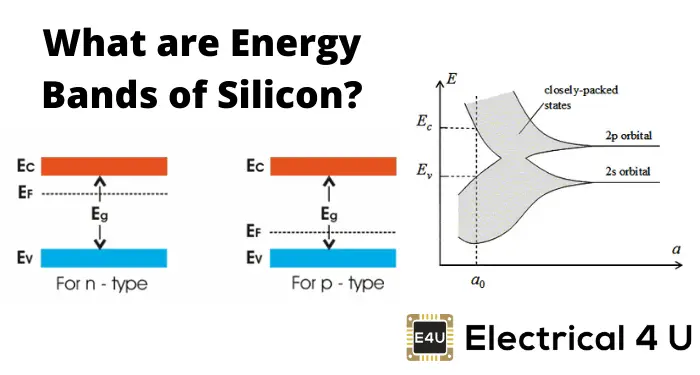
- N형 반도체: 5가 원소(예: 인, 비소)를 첨가하여 전도대 근처에 에너지 준위를 형성합니다. 이는 전자의 수를 증가시켜 전도성을 높입니다.
- P형 반도체: 3가 원소(예: 보론, 알루미늄)를 첨가하여 가전자대 근처에 에너지 준위를 만듭니다. 이는 정공의 수를 증가시킵니다.
3. 에너지 밴드 다이어그램의 중요성:
- 전자 이동과 전류 흐름: 에너지 밴드 다이어그램을 통해 전자와 정공의 이동 경로를 시각적으로 이해할 수 있습니다.
- 소자 동작 원리 이해: 다이오드, 트랜지스터 등의 반도체 소자의 동작을 설명하는 데 필수적입니다.
- 전기적 특성 예측: 밴드갭의 크기와 도핑 수준에 따라 물질의 전기 전도도를 예측할 수 있습니다.
페르미 준위에 대해 설명하세요.
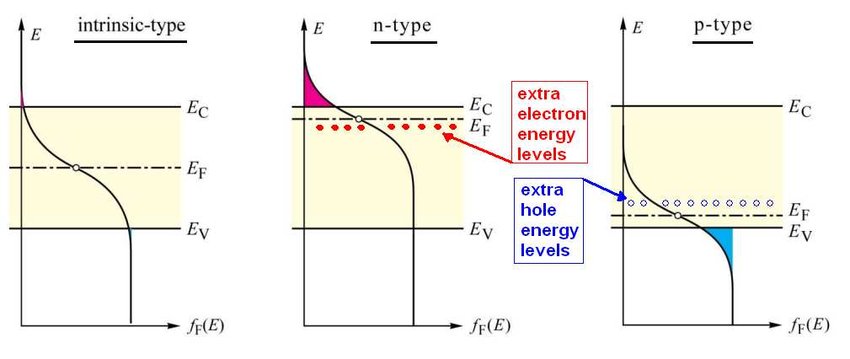
- *페르미 준위 (Fermi Level)**는 반도체 물리학에서 매우 중요한 개념으로, 에너지 상태가 전자로 채워질 확률이 50%인 에너지 준위를 의미합니다.
1. 기본 개념:
- 에너지 분포: 전자들은 에너지에 따라 특정 확률로 각 에너지 준위를 점유합니다. 이 확률 분포를 페르미-디랙 분포라고 합니다.
- 페르미 준위의 의미: 절대 영도(0K)에서 페르미 준위 아래의 에너지 준위는 모두 전자로 채워져 있고, 위의 준위는 비어 있습니다.
2. 반도체에서의 페르미 준위 위치:
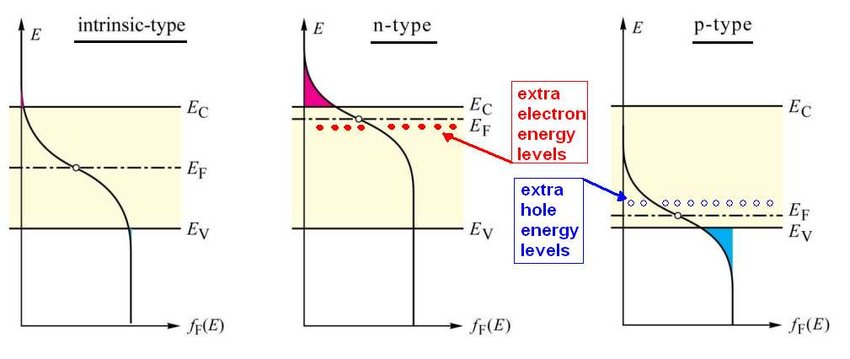
- 순수한 반도체 (Intrinsic Semiconductor): 페르미 준위는 가전자대와 전도대의 중앙에 위치합니다.
- N형 반도체:
- 도너(donor) 원소 첨가로 인해 전자 수가 증가합니다.
- 페르미 준위가 전도대 쪽으로 상승합니다.
- P형 반도체:
- 억셉터(acceptor) 원소 첨가로 인해 정공 수가 증가합니다.
- 페르미 준위가 가전자대 쪽으로 하강합니다.
3. 페르미 준위의 중요성:
- 전자와 정공 농도 결정: 페르미 준위의 위치에 따라 전자와 정공의 농도가 결정됩니다.
- 소자 특성 분석: PN 접합에서 전위 장벽과 전류 특성을 이해하는 데 필수적입니다.
- 온도 및 도핑 영향 분석: 온도 변화나 도핑 수준에 따른 전기적 특성 변화를 예측할 수 있습니다.
4. 에너지 밴드 다이어그램에서의 페르미 준위:
- 표시 방법: 에너지 축에 수평선으로 표시되며, 반도체의 종류와 상태에 따라 위치가 달라집니다.
- 온도 영향: 절대 영도가 아닌 실온에서는 페르미 준위 부근의 에너지 상태들이 부분적으로 점유됩니다.
5. 실용적 응용:
- 전자 소자 설계: 원하는 전기적 특성을 얻기 위해 페르미 준위의 위치를 조절합니다.
- 신뢰성 평가: 소자의 작동 온도 범위와 안정성을 분석하는 데 사용됩니다.
요약: 에너지 밴드 다이어그램과 페르미 준위는 반도체의 전기적 특성을 이해하고 소자를 설계하는 데 필수적인 개념입니다. 에너지 밴드 다이어그램은 전자들의 에너지 상태와 이동을 시각적으로 보여주며, 페르미 준위는 전자와 정공의 분포를 결정하여 반도체의 동작을 예측할 수 있게 합니다.
(실리콘) 반도체의 에너지 밴드 다이어그램을 설명하세요.
실리콘 반도체의 에너지 밴드 다이어그램은 반도체의 전기적 특성과 동작 원리를 이해하는 데 매우 중요합니다.
1. 에너지 밴드 구조:
- 가전자대 (Valence Band): 실리콘 원자의 최외각 전자들이 채워진 에너지 영역입니다. 이 전자들은 원자에 강하게 결합되어 있어 자유롭게 이동하지 못하며, 일반적인 조건에서는 전류에 기여하지 않습니다.
- 전도대 (Conduction Band): 가전자대보다 높은 에너지 상태로, 전자들이 자유롭게 이동할 수 있는 에너지 영역입니다. 여기의 전자들은 전류를 흐르게 하는 데 직접적인 역할을 합니다.
- 밴드갭 (Band Gap): 가전자대와 전도대 사이의 에너지 차이로, 전자가 가전자대에서 전도대로 이동하기 위해 극복해야 하는 최소 에너지입니다. 실리콘의 밴드갭 에너지는 약 1.12 eV입니다.
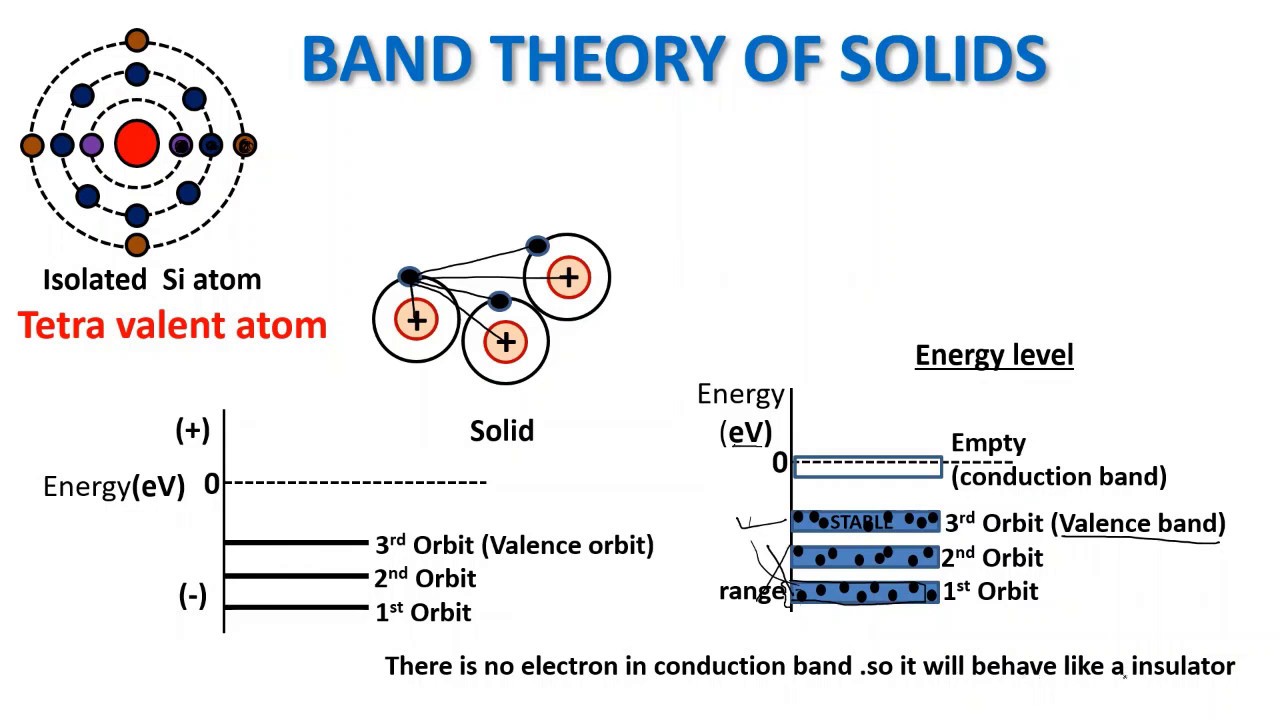
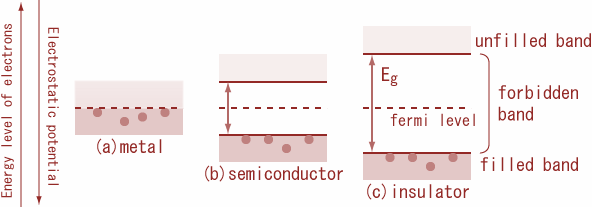
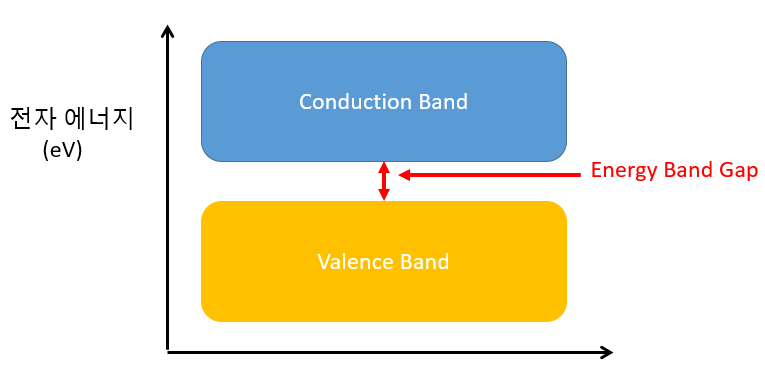
2. 에너지 밴드 다이어그램의 이해:
- 순수한 실리콘 (진성 반도체): 절대 영도에서는 가전자대가 전자로 완전히 채워져 있고 전도대는 비어 있습니다. 이 상태에서는 전기 전도성이 매우 낮습니다.
- 온도의 영향: 온도가 상승하면 열 에너지로 인해 일부 전자들이 밴드갭을 넘어 전도대로 이동합니다. 이에 따라 전도대에는 자유전자가, 가전자대에는 **정공(hole)**이 생성되어 전류가 흐를 수 있게 됩니다.
- 도핑 (Doping): 실리콘에 불순물을 첨가하여 전기적 특성을 조절할 수 있습니다.
- N형 반도체: 5가 원소(예: 인, 비소)를 첨가하여 전자의 수를 늘립니다. 이는 전도대 근처에 새로운 에너지 준위를 생성하여 전자가 쉽게 전도대로 이동할 수 있게 합니다. 결과적으로 페르미 준위가 전도대 쪽으로 상승합니다.
- P형 반도체: 3가 원소(예: 보론, 알루미늄)를 첨가하여 정공의 수를 늘립니다. 이는 가전자대 근처에 새로운 에너지 준위를 만들어 전자의 이동을 촉진합니다. 이 경우 페르미 준위가 가전자대 쪽으로 내려갑니다.
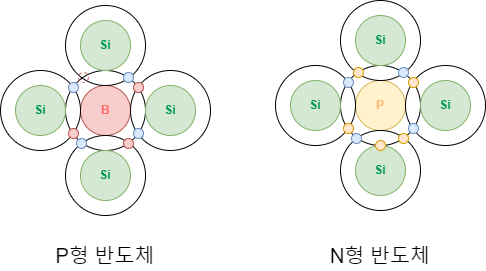
3. 에너지 밴드 다이어그램의 중요성:
- 전자 및 정공의 이동: 에너지 밴드 다이어그램을 통해 전자와 정공이 어떻게 이동하고 전류를 형성하는지 시각적으로 이해할 수 있습니다.
- 소자 동작 원리: 다이오드, 트랜지스터 등의 반도체 소자의 동작을 설명하는 데 필수적입니다.
- 전기적 특성 예측: 밴드 구조와 도핑 수준에 따라 반도체의 전기 전도도를 예측하고 제어할 수 있습니다.
페르미 준위에 대해 설명하세요.
- *페르미 준위 (Fermi Level)**는 반도체 물리학에서 매우 중요한 개념으로, 특정 온도에서 에너지 준위가 전자로 채워져 있을 확률이 50%인 에너지 수준을 의미합니다.
1. 기본 개념:
- 에너지 분포: 전자들이 에너지 준위를 점유하는 확률은 페르미-디락 분포에 따릅니다. 페르미 준위는 이 분포에서 점유 확률이 50%인 에너지 준위입니다.
- 절대 영도에서: 페르미 준위 아래의 에너지 준위는 모두 전자로 채워져 있고, 위의 에너지 준위는 비어 있습니다.
2. 반도체에서의 페르미 준위 위치:
- 진성 반도체 (Intrinsic Semiconductor): 순수한 실리콘에서는 페르미 준위가 가전자대와 전도대의 중앙에 위치합니다.
- N형 반도체:
- 도너 준위: 5가 원소를 도핑하면 전도대 근처에 에너지 준위가 생깁니다.
- 페르미 준위 이동: 전자의 수가 증가하여 페르미 준위가 전도대 쪽으로 상승합니다.
- P형 반도체:
- 억셉터 준위: 3가 원소를 도핑하면 가전자대 근처에 에너지 준위가 생깁니다.
- 페르미 준위 이동: 정공의 수가 증가하여 페르미 준위가 가전자대 쪽으로 하강합니다.
3. 페르미 준위의 중요성:
- 전하 운반자 농도 결정: 페르미 준위의 위치는 전자와 정공의 농도를 결정하며, 이는 반도체의 전기적 특성에 직접적인 영향을 미칩니다.
- 소자 동작 이해: PN 접합에서의 전위 장벽, 전류 흐름, 전압 특성 등을 분석하는 데 필수적입니다.
- 온도 및 도핑 영향 분석: 온도 변화나 도핑 농도에 따른 페르미 준위의 이동은 반도체의 동작과 성능에 큰 영향을 줍니다.
4. 에너지 밴드 다이어그램에서의 페르미 준위:
- 표시 방법: 에너지 밴드 다이어그램에서 페르미 준위는 일반적으로 가로로 그어진 점선으로 표시됩니다.
- 온도 영향: 온도가 상승하면 페르미 준위 부근의 에너지 준위들이 부분적으로 전자로 채워지거나 비게 됩니다.
5. 실용적 응용:
- 반도체 소자 설계: 원하는 전기적 특성을 얻기 위해 페르미 준위의 위치를 조절합니다.
- 전자 소자의 동작 원리 이해: 트랜지스터, 다이오드 등의 동작을 분석하고 설계하는 데 핵심적인 역할을 합니다.
이렇게 해서 실리콘 반도체의 에너지 밴드 다이어그램과 페르미 준위에 대해 설명드렸습니다.
(실리콘) 반도체의 에너지 밴드 다이어그램을 설명하세요.
반도체의 에너지 밴드 다이어그램은 가전자대, 금지대(밴드갭), 전도대로 구성되어 있습니다.
- 가전자대(Valence Band): 원자의 최외각 전자들이 채워져 있는 에너지 영역입니다. 이 전자들은 원자에 강하게 결합되어 있어 이동성이 낮고, 일반적으로 전류를 흐르게 하지 않습니다.
- 금지대(Forbidden Band): 가전자대와 전도대 사이의 에너지 영역으로, 전자들이 존재할 수 없는 에너지 범위입니다. 이 금지대의 폭은 **밴드갭(Band Gap)**이라고 불리며, 가전자대의 상단 에너지와 전도대의 하단 에너지의 차이를 의미합니다.
- 전도대(Conduction Band): 전자들이 자유롭게 이동할 수 있는 에너지 영역입니다. 이곳의 전자들은 전기 전도에 직접적으로 기여합니다.
에너지 밴드 다이어그램에서 **전자가 채워져 있는 가장 높은 에너지 준위가 바로 페르미 준위(Fermi Level)**입니다. 페르미 준위는 전자들의 에너지 분포를 나타내는 기준점으로, 반도체의 전기적 특성을 이해하는 데 중요합니다.
더 자세히 설명하면:
원자 수준에서 보면, 전자들은 특정한 에너지 준위를 가집니다. 원자 간 거리가 가까워지면 파울리의 배타 원리에 의해 전자들의 에너지 준위가 겹치지 않도록 조금씩 에너지 값이 달라지며, 이러한 에너지 준위들이 모여 밴드 형태를 이루게 됩니다.
실리콘의 경우, 원자 번호 14번으로 총 14개의 전자를 가지고 있습니다. 이 전자들은 에너지 준위를 채우는 과정에서 3s 오비탈 1개와 3p 오비탈 3개가 결합하여 sp³ 혼성 오비탈을 형성합니다. 이 혼성 오비탈들이 모여 가전자대를 구성하며, 각각의 오비탈에 전자가 채워집니다.
전도대는 3s와 3p 오비탈에 전자가 추가로 채워질 수 있는 에너지 상태로, 총 4개의 전자가 더 들어갈 수 있습니다. 따라서, 전도대는 전자들이 에너지를 받아 가전자대를 넘어 이동할 수 있는 영역이 됩니다.
요약하면, 실리콘 반도체의 에너지 밴드 다이어그램은 가전자대, 금지대(밴드갭), 전도대로 구성되며, 전자가 채워져 있는 가장 높은 에너지 준위가 페르미 준위이고, 금지대의 폭이 밴드갭입니다.
페르미 준위에 대해 설명하세요.
- *페르미 준위(Fermi Level)**는 특정 온도에서 에너지 상태가 전자로 채워져 있을 확률이 50%인 에너지 준위를 말합니다. 이는 전자들의 에너지 분포를 이해하는 데 중요한 기준점입니다.
- 절대온도 0K에서는 페르미 준위 아래의 에너지 준위는 모두 전자로 채워져 있고, 페르미 준위 위의 에너지 준위는 비어 있습니다.
반도체에서는 도핑과 온도 변화에 따라 페르미 준위의 위치가 변하게 됩니다.
- N형 반도체: 전자를 제공하는 도너(donor) 원소를 첨가하면 전자의 수가 증가하여 페르미 준위가 전도대 쪽으로 상승합니다.
- P형 반도체: 정공을 제공하는 억셉터(acceptor) 원소를 첨가하면 전자의 수가 감소하여 페르미 준위가 가전자대 쪽으로 하강합니다.
페르미 준위는 전하 운반자(전자와 정공)의 농도를 결정하며, 이는 반도체의 전기적 특성과 소자의 동작 원리에 직접적인 영향을 미칩니다.
요약하면, 페르미 준위는 에너지 밴드 다이어그램에서 전자가 채워져 있는 가장 높은 에너지 준위를 나타내며, 반도체의 도핑 상태와 온도에 따라 그 위치가 변합니다. 이는 반도체의 전기적 특성을 이해하고 제어하는 데 핵심적인 역할을 합니다.
1. 에너지 밴드 형성 과정
원자 수준의 에너지 준위
- 개별 원자에서의 에너지 준위:
- 전자들은 원자 내에서 특정한 에너지 준위를 가지는 궤도함수(오비탈)에 위치합니다.
- 에너지 준위는 낮은 에너지부터 높은 에너지까지 순서대로 채워지며, 각 준위에는 최대 전자 수가 제한되어 있습니다.
- 파울리의 배타 원리:
- 하나의 에너지 준위에는 두 개의 전자(스핀 방향이 반대인 전자)만 존재할 수 있습니다.
- 이는 전자들이 동일한 에너지 상태를 가질 수 없도록 제한합니다.
결정 구조에서의 에너지 밴드
- 원자 간의 상호작용:
- 개별 원자들이 가까워져서 결정 구조를 형성하면, 인접한 원자들의 전자 궤도함수들이 중첩됩니다.
- 이로 인해 에너지 준위가 분열하여 매우 많은 수의 에너지 준위들이 아주 작은 에너지 차이로 촘촘히 배열됩니다.
- 에너지 밴드의 형성:
- 분열된 에너지 준위들이 연속적인 에너지 범위를 이루어 에너지 밴드를 형성합니다.
- 결과적으로 개별적인 에너지 준위 대신, 전자들이 존재할 수 있는 에너지 영역(밴드)이 생깁니다.
2. 에너지 밴드 구조
가전자대 (Valence Band)
- 정의:
- 원자의 최외각 전자들이 채워져 있는 에너지 밴드입니다.
- 이 전자들은 원자와 강하게 결합되어 있어 이동성이 낮습니다.
- 특징:
- 가전자대가 완전히 채워져 있으면 전기 전도에 기여하지 못합니다.
- 온도 상승이나 외부 에너지에 의해 전자들이 전도대로 이동할 수 있습니다.
금지대 (Forbidden Band) 또는 밴드갭 (Band Gap)
- 정의:
- 가전자대와 전도대 사이에 존재하는 에너지 영역으로, 전자들이 존재할 수 없는 에너지 범위입니다.
- 특징:
- 밴드갭 에너지는 전자가 가전자대에서 전도대로 이동하기 위해 필요한 최소 에너지입니다.
- 밴드갭의 크기에 따라 물질이 도체, 반도체, 절연체로 구분됩니다.
- 도체: 밴드갭이 없거나 매우 작음.
- 반도체: 밴드갭이 중간 정도로, 전자 이동이 외부 조건에 따라 가능함.
- 절연체: 밴드갭이 매우 커서 전자 이동이 어려움.
전도대 (Conduction Band)
- 정의:
- 가전자대보다 높은 에너지 상태로, 전자들이 자유롭게 이동할 수 있는 에너지 밴드입니다.
- 특징:
- 전도대에 존재하는 전자들은 전기 전도에 직접적으로 기여합니다.
- 일반적으로 전도대는 비어 있거나 일부만 채워져 있습니다.
페르미 준위 (Fermi Level)
- 정의:
- 절대온도 0K에서 에너지 상태가 전자로 채워져 있을 확률이 50%인 에너지 준위입니다.
- 특징:
- 진성 반도체(Intrinsic Semiconductor): 페르미 준위는 밴드갭 중앙에 위치합니다.
- N형 반도체: 도너 원소의 도핑으로 전자 수가 증가하여 페르미 준위가 전도대 쪽으로 이동합니다.
- P형 반도체: 억셉터 원소의 도핑으로 정공 수가 증가하여 페르미 준위가 가전자대 쪽으로 이동합니다.
- 페르미 준위는 전자와 정공의 농도를 결정하며, 반도체의 전기적 특성에 큰 영향을 미칩니다.
3. 실리콘의 밴드 구조
실리콘의 전자 구조
- 원자적 특성:
- 실리콘(Si)은 원자 번호 14번인 4족 원소로, 최외각 껍질에 4개의 전자를 가지고 있습니다.
- 전자 배치:
- 전자 배치는 1s² 2s² 2p⁶ 3s² 3p²입니다.
- 최외각 전자인 3s와 3p 궤도함수는 에너지 준위가 비슷하여 혼성화가 일어납니다.
sp³ 혼성화 (sp³ Hybridization)
- 과정:
- 3s 궤도함수 1개와 3p 궤도함수 3개가 결합하여 4개의 sp³ 혼성 오비탈을 형성합니다.
- 결합 형성:
- 각 sp³ 혼성 오비탈은 하나의 전자를 가지고 있으며, 인접한 실리콘 원자와 공유 결합을 형성합니다.
- 이로 인해 실리콘은 4개의 공유 결합을 이루어 다이아몬드 구조의 격자를 형성합니다.
실리콘의 에너지 밴드 구조
- 가전자대와 전도대:
- 공유 결합에 참여하는 전자들의 에너지 준위가 모여 가전자대를 형성합니다.
- 가전자대 위에는 비어 있는 전도대가 존재합니다.
- 밴드갭:
- 실리콘의 밴드갭 에너지는 약 1.12 eV로, 전자가 가전자대에서 전도대로 이동하기 위해 필요한 에너지입니다.
- 이 밴드갭의 크기로 인해 실리콘은 반도체로서의 특성을 갖습니다.
- 전자 이동:
- 온도 상승이나 외부 에너지 공급(빛, 전기장 등)에 의해 전자들이 에너지를 받아 밴드갭을 넘어 전도대로 이동할 수 있습니다.
- 전도대로 이동한 전자는 자유전자로서 전기 전도에 기여합니다.
- 가전자대에 남은 빈 자리(정공)는 양전하를 띠며, 주변 전자들의 이동을 유도하여 전류 흐름에 참여합니다.
페르미 준위와 도핑
- 순수한 실리콘:
- 페르미 준위가 밴드갭의 중앙에 위치하며, 전도전자와 정공의 수가 동일합니다.
- 도핑을 통한 전기적 특성 제어:
- N형 반도체: 5가 원소(예: 인, 비소)를 도핑하여 전자의 수를 증가시킵니다. 페르미 준위는 전도대 쪽으로 이동합니다.
- P형 반도체: 3가 원소(예: 보론, 알루미늄)를 도핑하여 정공의 수를 증가시킵니다. 페르미 준위는 가전자대 쪽으로 이동합니다.
- 도핑을 통해 실리콘의 전기적 특성을 조절하여 다양한 전자 소자를 제작할 수 있습니다.
요약
- 에너지 밴드 형성 과정:
- 개별 원자의 에너지 준위들이 결정 구조에서 상호작용하여 연속적인 에너지 밴드로 형성됩니다.
- 에너지 밴드 구조:
- 가전자대, 금지대(밴드갭), 전도대로 구성되며, 전자들의 에너지 상태와 이동성을 결정합니다.
- 페르미 준위는 전자들이 채워져 있을 확률이 50%인 에너지 준위로, 반도체의 전기적 특성을 이해하는 데 중요합니다.
- 실리콘의 밴드 구조:
- 실리콘은 sp³ 혼성화를 통해 공유 결합을 이루며, 특정한 밴드 구조를 가집니다.
- 밴드갭이 1.12 eV로 적당하여 외부 에너지에 의해 전자 이동이 가능하며, 이는 반도체로서의 특성을 부여합니다.
- 도핑을 통해 전기적 특성을 제어하여 다양한 전자 소자의 구현이 가능합니다.
결론적으로, 반도체의 에너지 밴드 다이어그램은 전자의 에너지 상태와 이동을 이해하고, 이를 통해 물질의 전기적 특성을 파악하는 데 필수적입니다. 특히 실리콘의 밴드 구조와 sp³ 혼성 결합은 현대 전자 공학의 근간이 되는 중요한 개념입니다.